Table of contents
Open Table of contents
들어가며
조건: 행렬이 이며 n은 2의 거듭제곱
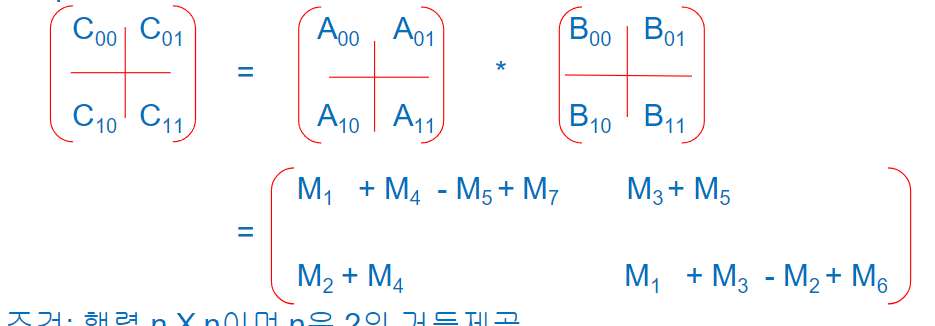 우리가 아는 일반적인 방법:
우리가 아는 일반적인 방법:
Strassen’s Matrix Multiplication (행렬 곱셈)
-
분할
- A, B 행렬을 분할
-
정복
- M1 ~ M7를 구하기 위해 재귀 호출
-
통합
- 최종 값 C를 구함
Formulas for Strassen’s Algorithm
python 코드
def default_matrix_multiplication(a: list, b: list) -> list:
"""
Multiplication only for 2x2 matrices
"""
if len(a) != 2 or len(a[0]) != 2 or len(b) != 2 or len(b[0]) != 2:
raise Exception("Matrices are not 2x2")
new_matrix = [
[a[0][0] * b[0][0] + a[0][1] * b[1][0], a[0][0] * b[0][1] + a[0][1] * b[1][1]],
[a[1][0] * b[0][0] + a[1][1] * b[1][0], a[1][0] * b[0][1] + a[1][1] * b[1][1]],
]
return new_matrix
def matrix_addition(matrix_a: list, matrix_b: list):
return [
[matrix_a[row][col] + matrix_b[row][col] for col in range(len(matrix_a[row]))]
for row in range(len(matrix_a))
]
def matrix_subtraction(matrix_a: list, matrix_b: list):
return [
[matrix_a[row][col] - matrix_b[row][col] for col in range(len(matrix_a[row]))]
for row in range(len(matrix_a))
]
def split_matrix(a: list) -> tuple[list, list, list, list]:
if len(a) % 2 != 0 or len(a[0]) % 2 != 0:
raise Exception("Odd matrices are not supported!")
matrix_length = len(a)
mid = matrix_length // 2
top_right = [[a[i][j] for j in range(mid, matrix_length)] for i in range(mid)]
bot_right = [
[a[i][j] for j in range(mid, matrix_length)] for i in range(mid, matrix_length)
]
top_left = [[a[i][j] for j in range(mid)] for i in range(mid)]
bot_left = [[a[i][j] for j in range(mid)] for i in range(mid, matrix_length)]
return top_left, top_right, bot_left, bot_right
def matrix_dimensions(matrix: list) -> tuple[int, int]:
return len(matrix), len(matrix[0])
def print_matrix(matrix: list) -> None:
print("\n".join(str(line) for line in matrix))
def actual_strassen(matrix_a: list, matrix_b: list) -> list:
if matrix_dimensions(matrix_a) == (2, 2):
return default_matrix_multiplication(matrix_a, matrix_b)
a, b, c, d = split_matrix(matrix_a)
e, f, g, h = split_matrix(matrix_b)
t1 = actual_strassen(a, matrix_subtraction(f, h))
t2 = actual_strassen(matrix_addition(a, b), h)
t3 = actual_strassen(matrix_addition(c, d), e)
t4 = actual_strassen(d, matrix_subtraction(g, e))
t5 = actual_strassen(matrix_addition(a, d), matrix_addition(e, h))
t6 = actual_strassen(matrix_subtraction(b, d), matrix_addition(g, h))
t7 = actual_strassen(matrix_subtraction(a, c), matrix_addition(e, f))
top_left = matrix_addition(matrix_subtraction(matrix_addition(t5, t4), t2), t6)
top_right = matrix_addition(t1, t2)
bot_left = matrix_addition(t3, t4)
bot_right = matrix_subtraction(matrix_subtraction(matrix_addition(t1, t5), t3), t7)
new_matrix = []
for i in range(len(top_right)):
new_matrix.append(top_left[i] + top_right[i])
for i in range(len(bot_right)):
new_matrix.append(bot_left[i] + bot_right[i])
return new_matrix
if __name__ == "__main__":
matrix1 = [[10, 8], [12, 11]]
matrix2 = [[4, 9], [8, 13]]
print(actual_strassen(matrix1, matrix2))
How to Run
python version: 3.11.6
Run main.py
pip install pipenv
pipenv --python 3.11.6
pipenv run python3 main.pyInput
하기 두 행렬을 곱함
matrix1 = [[10, 8], [12, 11]]
matrix2 = [[4, 9], [8, 13]]Output
[[104, 194], [136, 251]]Execution Image
